Problem of the N queens

List of boolean variables

2 variables: x1,x2

How can we express that exactly one of the 2 variables is true:
(x1⇒¬x2)∧(¬x1⇒x2)

How can we express that at most one of the 2 variables is true:
(x1⇒¬x2)

3 variables: x1,x2,x3

How can we express that exactly one of the 3 variables is true:
(x1->(¬x2∧¬x3))∧(¬x1⇒(x2⇒¬x3)∧(¬x2⇒x3))

How can we express that at most one of the 3 variables is true:
(x1->(¬x2∧¬x3))∧(¬x1⇒(x2⇒¬x3))

4 variables: x1,x2,x3,x4

How can we express that exactly one of the 4 variables is true:
(x1->(¬x2∧¬x3∧¬x4))∧(¬x1⇒(x2->(¬x3∧¬x4))∧(¬x2⇒(x3⇒¬x4)∧(¬x3⇒x4)))

How can we express that at most one of the 4 variables is true:
(x1->(¬x2∧¬x3∧¬x4))∧(¬x1⇒(x2->(¬x3∧¬x4))∧(¬x2⇒(x3⇒¬x4)))

N variables: x1,x2,...,xn

How can we express that exactly one of the n variables is true:
(x1->(¬x2∧..∧¬xn))∧(¬x1⇒...))

How can we express that at most one of the n variables is true:
(x1->(¬x2∧..∧¬xn))∧(¬x1⇒...))

Problem of the N queens

Put N queens on a chessboard NxN in such a way that none of the queens is in contact with another one:

Formalization

Each variable corresponds to one square. If the variable has the value true, this denotes that there is a queen inside the square.

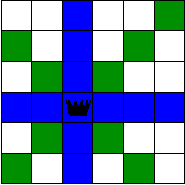
Example: N=3

Exactly one queen in each row:

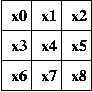
((x0⇒(¬x1∧¬x2))∧(¬x0⇒((x1⇒¬x2)∧(¬x1⇒x2)))) ∧
((x3⇒(¬x4∧¬x5))∧(¬x3⇒((x4⇒¬x5)∧(¬x4⇒x5)))) ∧
((x6⇒(¬x7∧¬x8))∧(¬x6⇒((x7⇒¬x8)∧(¬x7⇒x8)))) ∧

Exactly one queen in each column:

((x0⇒(¬x3∧¬x6))∧(¬x0⇒((x3⇒¬x6)∧(¬x3⇒x6)))) ∧
((x1⇒(¬x4∧¬x7))∧(¬x1⇒((x4⇒¬x7)∧(¬x4⇒x7)))) ∧
((x2⇒(¬x5∧¬x8))∧(¬x2⇒((x5⇒¬x8)∧(¬x5⇒x8)))) ∧

at most one queen in each diagonal:

((x0⇒(¬x4∧¬x8))∧(¬x0⇒(x4⇒¬x8))) ∧
(x1⇒¬x5) ∧
(x3⇒¬x7) ∧
((x2⇒(¬x4∧¬x6))∧(¬x2⇒(x4⇒¬x6))) ∧
(x1⇒¬x3) ∧
(x5⇒¬x7)

The resulting formula is not satisfiable: the problem does not have solution (one cannot put 3 queens in a chessboard 3x3).

Satisfiability

For dimension N, there are 2^(N*N) possible evaluations of variables. Thus, using the truth table to decide whether the problem is satisfiable is too costly. One can compute it till N=5. For bigger N, one has to find something better...

Monica Nesi