Davis-Putnam Algorithm
CNF formulae
Equivalences
-
We can express all the formulae in terms of the connectors
¬, ∧, ∨ only:
-
x⇒y is equivalent to ¬x∨y
x≡y is equivalent to (x∨¬y)∧(¬x∨y)
Order
A formula is CNF (conjunctive normal form) if it starts with the conjunctions,
after the disjunctions and finally the negations. In other words,
it is a conjunction of disjunctions of variables (possibly negated).
(x∨¬y)∧(¬x∨y) is CNF
(x∧¬y)∨(¬x∧y) is not CNF
Transformation
Every formula can be turned into an equivalent CNF formula.
-
First step: negations can be pushed down and possibly eliminated
(the first two equivalences are the so-called De Morgan's laws):
-
¬(x∧y) is equivalent to ¬x∨¬y
¬(x∨y) is equivalent to ¬x∧¬y
¬(¬x) is equivalent to x
-
Second step: conjunctions can be pulled before disjunctions
(using distributive laws):
-
x∨(y∧z) is equivalent to (x∨y)∧(x∨z)
(y∧z)∨x is equivalent to (y∨x)∧(z∨x)
Examples
Put the formula (x∨y)⇒z in CNF:
- Expand the implication: ¬(x∨y)∨z
- Push down the negations: (¬x∧¬y)∨z
- Pull the conjunctions before the disjunctions:
(¬x∨z)∧(¬y∨z)
Put the formula (x⇒y)⇒(z⇒t) in CNF:
- Expand the implication: ¬(¬x∨y)∨(¬z∨t)
- Push down the negations: (x∧¬y)∨(¬z∨t)
- Pull the conjunctions before the disjunctions:
(x∨¬z∨t)∧(¬y∨¬z∨t)
Exercises
*C6
Put in CNF the formula (x∨¬y)⇒z.
Satisfiability
Consider an example with the formula
(¬v1∨v3)∧(¬v1∨¬v2)∧(¬v3∨v2).
Using the truth table, we have the following execution:
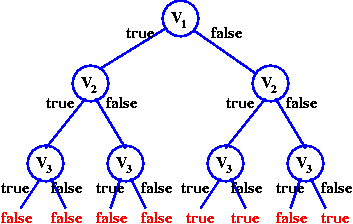
Contradictions
Because the formula is in CNF, we can derive beforehand when the formula
is false. In this example, once we have
v1=true and v2=true, it is not possible anymore to satisfy
the disjunction ¬v1∨¬v2. Thus, one can conclude
without considering v3:
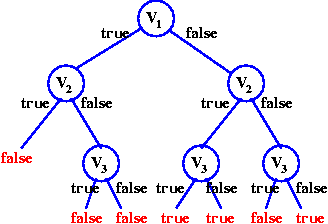
Unitary resolution
In fact, one can do slightly better. Once we have v1=true,
the only possibility to have ¬v1∨¬v2 is to have
v2=false. Also, to satisfy ¬v1∨v3 one needs
to have v3=true:
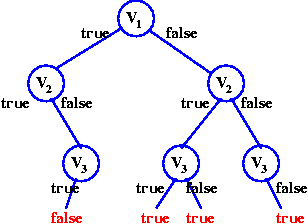
In a formula in CNF, the disjunctions contain only positive or negative
variables (x or ¬x).
In a disjunction, if all its signed variables (either positive or negative)
are false except one, this last one must be true.
Applying this single rule recursively is called "unitary resolution".
Using this resolution in the search for satisfiability is exactly what
Davis-Putnam algorithm does.
With a naive implementation of this algorithm, one can
verify the problem of the N queens till N=15.
Monica Nesi



