PARTE PRIMA: Algoritmi e Problemi

1/10/02:

Definizione di algoritmo. Input, output, correttezza, istanza, programma, pseudocodice. Algoritmo di ordinamento INSERTION SORT. Analisi di correttezza ed esempio.

Approfondimento: Algoritmo INSERTION SORT modificato per l'ordinamento non crescente e con visita invertita della sequenza.
Dispense: 1, 2, 3.
 

2/10/02:

Analisi di un algoritmo. Modello di calcolo RAM, misure di complessità statiche e dinamiche, dimensione dell'input. Analisi della complessità temporale dell'algoritmo INSERTION SORT. Caso migliore, caso peggiore, caso medio. Definizione di complessità asintotica. Notazioni $\Theta, O, \Omega$.

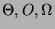Approfondimento: Algoritmo MAX-ELEMENTO per la ricerca dell'elemento massimo di un insieme dato ed analisi della complessità temporale.
Dispense: 4, 5, 6, 7, 8, 9.
 

8/10/02:

Notazioni 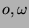$o, \omega$. Proprietà delle classi di complessità asintotica.

Approfondimento: Classificazione di 22 diverse funzioni in ordine non decrescente utilizzando le notazioni asintotiche $\Theta$ ed $o$.
Dispense: 10, 11, 12.
 

8/10/02:

Algoritmo SELECTION SORT: Caso migliore e caso peggiore. Confronto con l'INSERTION SORT. Relazione tra la complessità computazionale di un algoritmo e la delimitazione inferiore (lower bound) e superiore (upper bound) alla complessità di un problema. Ottimalità di un algoritmo. Esempi: ottimalità di MAX-ELEMENTO; problema del prodotto di due matrici quadrate.

Dispense: 13, 14, 15, 16, 17, 18.