PARTE SECONDA: Ordinamento in Tempo Ottimale

9/10/02:

Algoritmo di fusione di due sequenze ordinate: algoritmo sub-ottimale con complessità 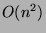$\Omega(n \log n)$ ed algoritmo ottimale con complessità $\Omega(n \log n)$.
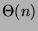Approfondimento: Algoritmo di ordinamento BUBBLE SORT. Ingegnerizzazione dell'algoritmo, caso migliore e caso peggiore.
Dispense: 19, 20, 21.

 

10/10/02:

Lower bound 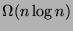$\Omega(n \log n)$ per il problema dell'ordinamento tramite confronti: albero di decisione, approssimazione di Stirling. Paradigma di programmazione divide et impera. Introduzione del MERGE SORT. Esemplificazione del suo funzionamento.

Dispense: 22, 23, 24, 25, 26, 27.

 

15/10/02:

Complessità computazionale del MERGE SORT e sua ottimalità.

Approfondimento: Innesto di INSERTION SORT all'interno di MERGE SORT. Complessità computazionale ed ottimalità in funzione della lunghezza delle sottosequenze ordinate tramite INSERTION SORT.

Dispense: 28, 29, 30, 31, 32, 33, 34.