Caratteristiche
base del Prolog
Stefania
Costantini
Corso
di Laurea in Informatica
Università
degli Studi di L’Aquila
Testo di riferimento:
I. Bratko, Prolog Programming far Artificial
lntelligence, Addison Wesley.
Programma: relazione
dati-risultati
Relazione calcolabile:
à descrizione finita
àin termini di un insieme finito di relazioni
fondamentali
à relazioni fondamentali: effettuabili
in modo finito
Linguaggi procedurali:
à descrizione passi per calcolare il risultato dai
dati
Linguaggi non procedurali:
à descrizione relazione da calcolare
Linguaggi non
procedurali
●
Linguaggi Funzionali (applicativi)
à lambda-calcolo
(Church, 1930)
(Schoenfinlkell, Curry,ecc.)
à notazione LISP (McCarthy, 1950)
à descrizione
computazione: funzioni e
composizione
● Linguaggi Logici
à calcolo
dei predicati dell’ 1°ordine (Frege, 1900)
(Horn, Robinson, ecc.
)
àProlog
(PROgramming in LOGic) .
(Kowalski e Colmerauer, 1970)
à descrizione
computazione: relazioni
Prolog: basato sul
linguaggio delle Clausole di Horm
Programmi Prolog:
● Fatti
● Regole
(o clausole)
● Quesiti
à Fatti
(o regole unitarie)
simpatico
(carlo).
amica
(anna,francesca).
padre
(giorgio,carlo).
studente
(nome (anna) , cognome (carletti) ).
r(t1
,...,tn).
r atomo
t1
,...,tn termini
termine il cui funtore
e' un predicato: atomo
Programmi Prolog:
Regole
simpatico (alberto ) :
- e_di_buon_umore (alberto) . amica(anna,francesca) :- gentile(francesca).
nonno (marco, carlo)
:- padre(marco, giorgio),
padre (giorgio,carlo) .
A :- B1,...,Bn
A, B1,...,Bn atomi
à A se B1 e
... Bn
à se
valgono B1 ... Bn
allora vale anche A
à e se
non valgono B1 ... Bn ? Non sappiamo se vale A, che
potrebbe derivare da altre regole
à
Quindi, regola del programma considerata come Regola di Inferenza: da B1 ... Bn derivo
A
à Non
si applica il contropositivo:
se non valgono B1 ...
Bn non
derivo Ø A
Significato di fatti e
regole: Relazioni
Relazione
n-aria R su dominio D:
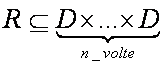
R si
può rappresentare mediante un predicato p dove:
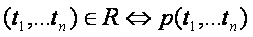
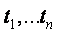 sono termini
sono termini
In Prolog:
fatti: asseriscono
incondizionatamente l'appartenenza di una n-upla ad una relazione
amico
(carlo, paolo) .
regole:asseriscono l'appartenenza
di una n-upla ad una relazione in base a certe condizioni
amico(gianni,anna):-
simpatica(anna).
Programmi Prolog:
à Quesiti
(o Query)
simpatico (carlo) .
amica (anna, francesca)
.
padre (giorgio, carlo)
.
studente(nome(anna),
cognome(carletti)).
?- simpatico(carlo).
yes
?-amica (anna, francesca).
yes
?-amica (anna, marina).
no
Quesito: ?-G1,...,Gn con G1 ,...,Gn atomi
Programmi Prolog:
à Quesiti
simpatico (carlo) .
amica (anna,
francesca) .
padre (giorgio, carlo).
studente (nome (anna),
cognome (carletti) ) .
?- simpatico(carlo),
amica(anna,francesca).
yes
?-amica (anna, francesca), simpatico(carlo).
yes
?-simpatico(carlo), amica(anna,marina).
no
?-giovane (carlo) .
no
?-amica
(anna, francesca).
no
Programmi Prolog:
à Regola
nonno (marco, carlo) :- padre(marco,
giorgio),
padre
(giorgio,carlo).
padre ( alfredo, giovanni).
padre (marco, giorgio).
madre(anna, giorgio).
padre (giorgio, carlo).
?-nonno (marco,
carlo).
----------------------------------->1
padre(marco, giorgio)
----------------------------------->2
padre(giorgio, carlo)
·
Dichiarativamente:
predicato definito in funzione di altri predicati.
·
Pragmaticamente:
o
Regola:
definizione di procedura
o
Quesito:
chiamata della procedura
=>
chiamata (in ordine) delle procedure
nella definizione
Programmi Prolog:
à
Quesiti con variabili
nonno (marco, carlo) :- padre(marco, giorgio),
padre(giorgio,carlo).
padre (alfredo, giovanni).
padre (marco, giorgio).
madre(anna, giorgio).
padre (giorgio, carlo).
?-padre:(X,carlo).
X = giorgio
?-padre
(giorgio, Y).
Y = carlo
?-
padre(X,Y) .
X = alfredo, Y =
giovanni ;
X = marco, Y = giorgio;
X = giorgio, Y = carlo
Relazioni con
variabili
Una variabile prende il posto di un
generico termine.
ð
usando variabili, un singolo fatto o regola
prende il posto di più asserzioni
amico (gianni,X):- simpatico (X) .
* qualsiasi sia X,
se X e' simpatico allora X e' amico di giorgio
à la variabile X si intende quantificata
universalmente
Tutte le istanze di X
nella stessa clausola (fatto o regola) si riferiscono allo stesso oggetto
Se la variabile X
compare in un' altra clausola, va considerata una variabile diversa.
Le variabili possono
essere legate a termini mediante il meccanismo di unificazione.
Relazioni
con variabili
nonno(X,Z):-
padre(X,Y), padre(Y,Z).
nonno(X,Z):-
padre(X,Y) , madre(Y,Z).
padre(john,bill)
.
padre (bill,mary)
.
Lettura
Per tutti i termini X e Z, X
e' il nonno di Z se
 esiste un termine Y tale
che X è il padre di Y
esiste un termine Y tale
che X è il padre di Y
e Y è il padre di Z
oppure
 esiste un termine Y tale che X e' il
padre di Y
esiste un termine Y tale che X e' il
padre di Y
e Y e' la madre di Z
?-nonno (X, Y) .
Lettura
Esistono due termini X e Y
tale che X e' il nonno di Y?
Quesiti
con variabili
nonno(X,Z):- padre (X,Y) , padre(Y,Z).
nonno(X,Z):-
padre(X,Y), madre(Y,Z).
padre (john, bill).
(1)
padre (bill,
mary) . (2)
padre (bill,
thom). (3)
padre
(thom,chris). (4)
madre(mary,june). (5)
?-nonno (X, Y) .
X = john, Y = mary; /*1+2*/
X = john, Y = thom; /*1+3*/
X = mary, Y = june; /*2+5*/
X = bill, Y = chris; /*3+4*/
no (non
si trovano latri risultati)
Nota: Le
variabili logiche non possono essere riassegnate! Durante una computazione, se
vengono istanziate mantengono lo stesso valore fino al raggiungimento di un
risultato.
Se si richiede (col
‘;’) di cercare un’altra soluzione, allora vengono disistanziate e (se
possibile) reistanziate a valori diversi.
Caratteristiche
base del Prolog:
Unificazione
Risoluzione
Definizioni
ricorsive
Stefania
Costantini
Stefania
Costantini
Corso
di Laurea in Informatica
Università
degli Studi di L’Aquila
Prolog: linguaggio
delle clausole di Horn
Elementi principali:
·
termini
·
atomi
·
fatti
e regole
Un termine (o atomo)
puo' essere:
v una
costante
(ad es. pippo r2d2
524 mia_cost)
v una
variabile (V, X, Pippo, JK_234)
v una struttura
Una struttura e'
composta da:
 funtore n-ario (simbolo di predicato o
funzione)
funtore n-ario (simbolo di predicato o
funzione)
 n termini come argomenti
n termini come argomenti
Descrizione dei Dati
in Prolog
Strutture dati del Prolog: Termini
 Atomi
Atomi
 Variabili
Variabili
 Strutture
Strutture
Costanti:
nomi di oggetti, funzioni, relazioni, denotano elementi del dominio di
interesse
Ø Sequenza
di lettere, cifre e ‘_’
Ø Primo
carattere: lettera maiuscola
Esempi:
giorgio
r2d2
1524
mio_atomo1
Numeri: atomi particolari con operazioni
predefinite
Descrizione dei Dati in
Prolog,
● Variabili: identificatori
che denotano oggetti
v sequenza
di, lettere, cifre e '-'
v primo
carattere:: lettera maiuscola
Esempi:
V
L1
Antenato
Loc_var
Pippo
_ 1
Descrizione dei Dati
in Prolog
● Struttura: oggetto gerarchico
à organizzato ad albero, composto da
o
nome (funtore)
o
argomenti
compositore (bach)
compositore(nome(berlioz), nazionalita(francese)).
compositore (nome (george,gershwin) , nazionalita
(americana) ,
composizione
(rapsodia_in _blu) ).
compositore (verdi, opere (aida, traviata, rigoletto).

Descrizione dei Dati
in Prolog
Riassumendo:
à Un
termine può essere:
 una costante
una costante
(ad es. pippo
r2d2 524 mio_atomo)
 una variabile
una variabile
 una struttura
una struttura
à Una
struttura e' composta da:
v funtore n-ario
v n
termini come argomenti
Unificazione
governa il procedimento di
istanziazione delle variabili
E' un procedimento che
tenta di rendere uguali due
termini,eventualmente istanziando le variabili in essi contenute
·
due
costanti unificano se sono uguali
·
due variabililii unificano (condivisione)
·
una
variabile ed un termine unificano istanziando la variabile al termine
·
due
strutture unificano se:
 hanno lo stesso funtore
hanno lo stesso funtore
 hanno lo stesso numero di argomenti (arità)
hanno lo stesso numero di argomenti (arità)
 gli
argomenti corrispondenti unificano
gli
argomenti corrispondenti unificano
Esempi
|
a
|
a
|
unificano
|
|
f(a)
|
f(a)
|
unificano
|
|
g(f(a))
|
g(f(a))
|
unificano
|
|
V
|
a
|
unificano con V/a
|
|
X
|
g(s)
|
unificano con X/g (5)
|
|
X
|
Y
|
unificano con X/Y (o Y/X)
|
|
f(a)
|
f(R)
|
unificano con A/a
|
|
f(X)
|
f(Y)
|
unificano con X/Y (o Y/X)
|
|
p(a,X)
|
p(Y,c)
|
unificano con X/c e Y la
|
|
p(a,X)
|
p(Y,f(c))
|
unificano con X/f(c) e V/a
|
|
q(f(X),a)
|
q(f(b),V)
|
unificano con X/b e V/a
|
L'insieme
delle sostituzioni Variabile/termine ottenute unificando due strutture si dice unificatore
delle strutture
Unificatore più generale
L’
Unificatore più generale (Most general Unifier, o mgu) e’ quello che
produce il minor numero possibile di istanziazioni, ossia non fa “ipotesi” non
strettamente necessarie sul valore delle variabili.
p(X,R,V,a)
e p(f(b),Y,Z,K)
Un unificatore: {X/f(b), R/Y/pippo, V/Z, K/a}
Un altro unificatore: {X/f(b), R/Y/minnie,
V/Z/paperina, K}
Lo mgu: {X/f(b), K/a}
Nel linguaggio delle clausole di Horn (e in Prolog)
lo mgu esiste sempre ed è unico
Applicazione degli
unificatori
Gli unificatori in genere
sono indicati con lettere greche, ad es. δ. L'applicazione di un unificatore δ
ad un termine t è indicata con tδ, e produce un nuovo termine t' in cui sono
state effettuate tutte le sostituzioni variabile/valore indicate in δ.
Nell'esempio precedente,
se t1 =
p(X,R,V,a) e
p(f(b),Y,Z,K),
ed
inoltre δ1 = {X/f(b), R/Y/pippo, V/Z, K/a}
e
δ2 = {X/f(b), R/Y/minnie,
V/Z/paperina, K}
si ha
t1 δ1 = t2 δ1 = p(f(b),pippo,V,a)
Indifferentemente, p(f(b),pippo,Z,a) perchè V e Z sono in condivisione.
Questo
vuol dire che se l'unificazione è utilizzata durante il processo
di
dimostrazione di una query, il valore preso dall'una sarà assunto
anche
dall'altra.
t1 δ2 = t2 δ2 = p(f(b),
minnie, paperina, a)
Lo mgu di indica di solito
con s.
t1
s = t2
s = p(f(b), R,
V, a) = p(f(b), Y, Z, a)
Risoluzione
Se A:-B1,...,Bn e
B1,...,Bn sono veri allora A e' vero
Dalle clausole:

Si derivano per risoluzione mediante
unificazione
amico (gianni, carlo)
amico (gianni,
giacomo)
Quesiti (o query)
|
?-amico(Gianni,Y).
|
Esistono dei valori
per cui valga amico(Gianni,Y)?
|
|
?-amico(X,Y).
|
Esistono
dei valori per cui valga amico(X,Y)?
|
Le variabili nei quesiti sono quantificare esistenzialmente.
Risposte ai quesiti
Il quesito, o query, o goal
?-G
e' dimostrato (riceve risposta positiva) se:
 Esiste una clausola A:-B1,…,Bn dove G e A
unificano
Esiste una clausola A:-B1,…,Bn dove G e A
unificano
 Si riesce a dimostrare B1,…,Bn
Si riesce a dimostrare B1,…,Bn
La risposta al quesito può essere:
à
"yes" oppure "no'" se G non contiene variabili
à la
sostituzione ottenuta per le variabili di G
?-amico(gianni, Y) .
ha due risposte:
>> X/carlo
>> X/giacomo
Definizioni
ricorsive
Utilizzano la
relazione che si sta definendo nel corpo della definizione stessa
Rendono possibile descrivere ogni funzione
calcolabile mediante un numero finito di regole
(due regole permettono di generare tutti i numeri
naturali...)
Struttura di una definizione ricorsiva:
Ø passi
base: casi semplici per cui il risultato e' noto
Ø passi
ricorsivi: il risultato viene definito come combinazione di risultati parziali
calcolati su termini più semplici
Definizioni
ricorsive: i numeri naturali
Procedura nat(X) <=> X e' un
numero naturale
nat(O).
nat (suc (X) ) :- nat (X) .
In questa rappresentazione:
1 e ' rappresentato come suc(0)
2 e' rappresentato come suc(suc(0))
………
Procedura somma (X, Y, Z) <=> la
somma di X e Y è Z
somma(X,O,X):-
nat(X).
somma(O,X,X):- nat(X),
somma (suc (X) ,suc
(Y) ,suc (suc (Z))) :-
nat(X) , nat(Y) , somma(X,Y,Z).
Strategia depth-first
(ricerca in profondità)
La strategia
depth-first non e' fair, e quindi non e' completa
Motivo: seleziona
sempre la sottometa più a sinistra, e usa sempre la prima clausola
Se questa combinazione
causa un loop non riesce a uscirne
a(X,Y) :-a(X,Z)
,a(Z,Y).
a(a,b).
a (b,c).
M = {a(a,b) , a(b,c), a(a,c)}
?-a(a,c) , /*Loop*/
a(a,b). %
passi base della ricorsione
a(b,c). %
sempre per primi
a(X,Y) :-a(X,Z), a(Z,Y).
?-a(a,d)
, /*Loop* /
Nota: si
adotta la depth-first per ragioni di efficienza, contando sul programmatore per
prevenire i loop
Semantica (per grandi
linee) del linguaggio delle clausole di Horn
Modello di un
programma: sottoinsieme della Base dove tutte le clausole del programma sono
vere
clausole = fatti o
regole (quantificati universalmente)
A:-B1,...,Bn.
C.
* Un fatto C e' vero
in ogni modello
* Una regola
A:-B1,...,Bn e' vera in un modello se
·
Sia A
che B 1 , . . . , Bn sono in modello
·
B1,...,Bn
non sono nel modello (A può esserci o meno)
Nota: se
una proposizione A contiene variabili, dire
"A
è nel modello"
significa
che il modello contiene tutte le istanze di A ottenute sostituendo le
variabili con termini chiusi (o round, ossia privi di variabili)
Modello minimo
p(a).
q (b).
q (X) : -p (X)
Questo programma ha
più di un modello:
p(a),
q(a), q(b) M1
p(a), q(a), q(b), p(b) M2=Base di P
M1 è
"migliore"', perché è totalmente
determinato da P
In generale: i modelli
di ogni programma hanno una intersezione, il modello minimo
Il modello minimo contiene
tutte e sole le conseguenze logiche del programma, ossia le proposizioni
la cui verità è determinata dalla verità delle clausole del programma
Il modello minimo si
può calcolare come funzione del programma
Calcolo del modello
 Inserisci nel modello tutti i fatti
Inserisci nel modello tutti i fatti
(o tutte le loro istanze se non sono
ground)
 Ripeti fino a che e' possibile:
Ripeti fino a che e' possibile:
inserisci nel modello
la testa di una regola
quando il corpo è già presente
Esempio: modello
finito
Programma
p (a).
q (b) .
q (X) :-p (X).
Costruzione
del Modello
ü p(a)
q(b)
ü q (a)
Modello
Minimo
M = {p(a),q(b),q(a)}
Esempio: modello
infinito
Programma
nat(0).
nat (suc (X) ) :
-nat (X) .
Costruzione del modello
Minimo
ü nat(0)
ü nat(suc(0)
nat
(suc (suc (0))
nat (suc (suc (suc (0) ) ) )
nat (suc (suc (suc (suc (0) ) ) ) )
…
Modello
Minimo
M =
{nat(0),nat(suc(0)),nat(suc(suc(0))), . . .}
Clausole il Logica del Prim’Ordine
(First Order Predicate Logic, FOPL)
A:-B1,...,Bn.
sta per
A Ü
B1,...,Bn (implicazione
logica)
ossia
A Ú ØB1 Ú … Ú ØBn
dove “Ú” è
la disgiunzione e “Ø” la
negazione
A,B1,...,Bn
sono chiamati “atomi” o “letterali positivi” mentre i “ØBn” sono “letterali negativi”
Questa è una clausola di Horn perché
contiene un solo letterale positivo.
Risoluzione in FOPL fra clausole di Horn
·
Clausole
ground
A Ú ØC
ØA Ú ØB
_______
ØC Ú ØB
Concetto sottostante:
A e ØA sono sempre uno vero e uno
falso. Entrambe le disgiunzioni date però si assumono essere vere. Allora, se A
è falso ØC dovrà essere vero. Invece, se A è vero (e
quindi ØA è falso) ØC dovrà
essere vero. Non sapendo quale dei due casi si presenterà di volta in volta, si
sa però che o ØC o ØB dovrà essere vero, il che formalmente significa
che la disgiunzione ØC Ú ØB
dovrà essere vera.
Analogamente se B e C
sono
disgiunzioni di
letterali negativi
·
Clausole
non ground: se s è lo
mgu di A1 ed A2, ossia A1s = A2s, allora
A1 Ú ØC
ØA2 Ú ØB
_________
(ØC Ú ØB)s
Risoluzione
in FOPL fra clausole di Horn
Caso particolare:
A
ØA
_______
clausola
vuota
contraddizione!
Concetto sottostante: A e ØA sono sempre uno vero e uno falso, per cui avere
(soltanto) A e ØA vuol dire essere caduti in contraddizione (che
formalmente si esprime con la clausola vuota)
Esempio:
Base
di conoscenza (round)
ØA (1)
A Ú ØB (2)
B (3)
Da 1 e 2 si deriva per
risoluzione
ØB (4)
da 3 e 4 si deriva la
clausola vuota (contraddizione!)
Risoluzione in Prolog
Esempio precedente:
A Ú ØB
B
in Prolog si scrive
A :-
B. (2)
B. (3)
Inoltre, ØA è
una query, indicata con ?-A. (1)
Essa riesce esattamente con i passi mostrati
sopra: dalla query (1) e dalla clausola (2) si deriva la nuova query
?- B (4) che sta per ØB.
Dalla nuova query e dalla clausola (unitaria) (3)
si arriva alla clausola vuota, e la query è dimostrata.
Formalmente, fare una query vuol dire asserire la
negazione della query stessa. Se per risoluzione si arriva alla clausola
vuota, ossia ad una contraddizione, allora la query è dimostrata per
assurdo.
Proprietà della
Risoluzione
Come si comporta la risoluzione, rispetto al
Modello Minimo?
Ossia, data la query
?-p (Arg1,.. ,
Argn)
il successo o fallimento è in relazione con
l'appartenenza di p (Arg1,..,Argn) al
Modello minimo?
Risposta: La
risoluzione corretta e completa rispetto al Modello Minimo di un programma
 E' corretta: tutte le proposizioni dimostrabili
mediante risoluzione appartengono al modello minimo (sono conseguenze logiche
programma)
E' corretta: tutte le proposizioni dimostrabili
mediante risoluzione appartengono al modello minimo (sono conseguenze logiche
programma)
 E' completa: tutte le proposizioni che
appartengono al modello minimo sono dimostrabili mediante risoluzione (ad una
condizione!)
E' completa: tutte le proposizioni che
appartengono al modello minimo sono dimostrabili mediante risoluzione (ad una
condizione!)
Condizione
per la completezza: la strategia di risoluzione deve essere
"fair"!!!
Cioè: ogni sottometa
deve prima o poi essere risolta utilizzando ogni possibile clausola. La
depth-first non è fair, sta al programmatore evitare i loop!
Descrizione dei Dati
in Prolog
●Lista: caso
particolare di struttura
[pippo, pluto, c123,
f(a)]
● notazione [. . . ]
àabbreviazione
per strutture con funtore ‘.’
. (pippo, . (pluto, .
(c123, . (f(a) , []))))
● [] è un atomo
speciale che sta per la lista vuota
● Liste
à primo elemento: testa (head)
à lista elementi rimanenti: coda, o corpo (tail)
[pippo | [pluto, c123, f(a)]]
[pippo, pluto | [c123, f(a)]]
[pippo, pluto, c123, f(a) | [] ]
Descrizione dei Dati
in Prolog
 Liste: simbolo speciale ‘|’
Liste: simbolo speciale ‘|’
separa i primi n elementi dalla
lista dei rimanenti
[ E1,…,En | [...] ]
|
[anna, carla]
|
=
|
[anna,
carla | [] ]
|
|
[anna,
carla]
|
=
|
[anna
| [carla] ]
|
|
[anna,
carla]
|
=
|
[anna
| [carla | [] ]
|
|
[anna,
carla]
|
=/=
|
[anna
| carla]
|
|
[anna,
carla]
|
=/=
|
[
[anna, carla] ]
|
|
[anna,
carla]
|
=/=
|
[anna,
carla, [] ]
|
 Uso delle
liste nei termini:
Uso delle
liste nei termini:
compositori(nazionalità(tedesca),
[bach,mozart,brahms]).
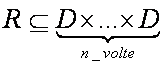
![]()
![]() sono termini
sono termini
