Caratteristiche base del Prolog:
cut, Efficienza,
Negazione
e
Significato
Logico
dei Programmi,
Predicati
Meta-logici ed
Extra-Logici
Stefania
Costantini
Dipartimento
di Informatica, Università degli Studi di L’Aquila
Il predicato predefinito
di taglio '!', o 'cut'
Effetto: ha sempre successo, non viene mai risoddisfatto
Funzione:
inibisce il backtracking
Come: congelando
le scelte effettuate sulla meta genitrice
Meta
genitrice: e' la meta che e' stata risolta mediante Ia clausola contenente il !
Usi del cut
1) Efficienza: per evitare tentativi inutili di unificazione
(tipicamente: base della ricorsione)
2) Per
evitare la ricerca di soluzioni alternative
- inesistenti
- non volute
3) Per
evitare computazioni che non terminano, in presenza
- di infinite
soluzioni
- di potenziali cicli infiniti
4) Per creare strutture di selezione
5) Per far fallire la meta genitrice
6) Per
realizzare la negazione per fallimento
Esempi di uso del cut
v Efficienza
+ prevenzione ciçlo infinito
(nella seconda clausola manca un test!!!)
fattoriale(O,1):-
!
fattoriale(N,F):-
N1 is N1-1, fattoriale(N1 ,F1), . F is N*F1.
v Forzare
un' unica soluzione
appartiene (E,
[E|C]):-!.
appartiene (E,
[_|C]): - appartiene(E,C).
In
questo caso, altre soluzioni:
- non
esistono se la lista ha elementi distinti
-
altrimenti, possono esistere ma sono ininfluenti
v Forzare
un' unica soluzione
ha_figli (X)
: - figlio (X, Y) , ! .
"X
ha figli se esiste Y che e' figlio di X"
Esempio
a(X):-
b(X). [1]
a (X)
: - c (X) , ! , d (X) , e (X) . [2]
a(X):-
f(X). [3]
?-a(V).
o Si
seleziona [1]
o Se b(X) fallisce si seleziona [2]
o Se c(X) fallisce si seleziona [3]
o Se
c(X) riesce si esegue!, d (X)
o Se d(X) riesce si esegue e(X)
o Se d(X) fallisce
- non
si ritenta c(X)
- non si
seleziona [3]
quindi la meta
genitrice a(V) fallisce
o Se e(X) fallisce
- si ritenta solo
d(X), ma non c(X) ne' si seleziona [3] quindi la meta genitrice a(V) fallisce
Uso dell' Unificazione nelle definizioni
definisco
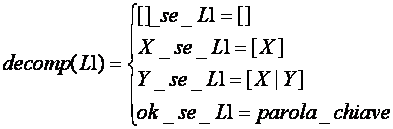
In Prolog: decomp(L1, L2)
decomp ( [], []).
decomp ( [X], X).
decomp([X|Y], Y).
decomp (parola_chiave, ok).
?-decomp([]
,L2).
L2 = [].
? - decomp (L 1 ,5).
L1
= [5]
?- decomp([aa,
bbb, cc], L2).
L2 = [bbb, cc]
decomp (parola_chiave,
L2).
L2 = ok
Ricorsione ed
efficienza
Esempio: trovare l’ elemento minimo Min e l'elemento
massimo Max di una lista data L.
minmax ( ?Min, ?Max,
+Lista)
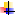 passo base: lista di un solo elemento
passo base: lista di un solo elemento
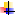 passo ricorsivo : lista non vuota,
minimo e massimo provvisori
passo ricorsivo : lista non vuota,
minimo e massimo provvisori
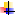 relazione ausiliaria: min(+X,+Y,?Z) trova il minimo
fra due elementi
relazione ausiliaria: min(+X,+Y,?Z) trova il minimo
fra due elementi
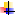 relazione ausiliaria: max(+X, +Y, ?Z)
trova il massimo fra due elementi
relazione ausiliaria: max(+X, +Y, ?Z)
trova il massimo fra due elementi
minmax (X,
X, [X]):-!.
minmax(Min, Max, [X|L]):- minmax(MinL, MaxL,
L),
min(X, MinL,Min),
max (X, MaxL,
Max).
Problema: se la lista
è lunga N, le N-1 chiamate a minmax fino a
raggiungere il passo base restano in sospeso
Conseguenza: poiché ad
ogni chiamata di procedura e' associato un record di allocazione,
si consuma molto spazio.
Soluzione:
procedura ausiliaria con parametri addizionali per propagare fra le successive chiamate i risultati parziali
minmax1 (?Min, ?Max, +Lista, ?PMin, PMax)
PMin e PMax
sono il minimo e massimo provvisori, ossia quelli trovati fino a quel punto.
Ma minmax1
va chiamata con due parametri in più!
soluzione: mascherare
la presenza di minmax1
minmax (X, X,
[X]):-! .
minimax(Min, Max, [X|L]) :- minimax1(Min, Max, L, X, X).
Minmax1(PMin,
PMax, [], Pmin, PMax):-!.
Miinmax1(Min, Max, [X|L], PMin,
PMax):-
min (X, Pmin, X), !,
minmax1(Min, Max, L, X, PMax) .
minmax1 (Min, Max, [X|L], PMin, PMax):-
max(X, Pmax, X),
minmax1(Min, Max, L, PMin,X).
Definizioni ricorsive: Esercizi sulle liste
Append
append ([] ,L,L) :- !.
append([A|X], Y, [A|Z]):- append(X, Y, Z).
Prefisso
prefisso(P, L):-
append (P, _ ,L).
oppure
prefisso ([]
,L):- !.
prefisso([A|P], [A|C]):- prefisso(P,C).
Suffisso
suffisso
(L,L):- !.
suffisso (S,
[_|L]):- suffisso(S, L).
Esercizio da svolgere:
Definire una relazione
ternaria scomponi(P, S, L) che è vera se S è una sottolista di L
e P è la lista di elementi che precedono S
in L
Ad
esempio vale:
scomponi ( [c, r, p],
[q, g, s], [c, r, p, q, g, s, u, d, f])
Esercizio da svolgere:
Definire
una relazione ripulisci che rimuove da una lista data tutte le occorrenze
contigue dello stesso elemento, trasformando ad esempio la lista::
[lista, lista, prova,
prova, con, elementi, elementi, duplicati]
nella
lista
[lista, prova, con,
elementi, duplicati]
Negazione in Prolog
not(G) o
\+ G
il not è un predicato metalogico
che rappresenta la negazione per fallimento
not(G) riesce se G fallisce come meta Prolog
Proceduralmente:
not(G):- G, !, fail.
not(_).
Importante: il
successo di not(G) non può produrre risultati!
o not(G) fallisce se G
riesce
o
not(G)
riesce se G fallisce:' ma 1Ln1n181 mieta che fallisce non
istanzia
variabili
Quindi, not(G) in
Prolog
e' solo un test sulla riuscita o fallimento
di G.
Per non creare problemi, not(G)
deve essere "ground" (non
possono esservi in G variabili non istanziate)
Altrimenti: si possono avere risultati anomali
animale
(gatto) .
vegetale
(melanzana) .
La meta
?-vegetale (X), not(animale(X)
) .
riesce. Infatti:
- vegetale (X) produce
il risultato X/melanzana
- not (animale
(melanzana) ) riesce
Invece la meta
?-not(animale(X)
) , vegetale (X) .
fallisce!
Infatti, la
prima sottometa
- not(animale(X)) fallisce
perché animale(X) riesce con X/gatto
Eppure, le
due mete sono logicamente equivalenti!
Se una meta not(G) non e' completamente istanziata,
l'and logico (“,”) non e' piu'
commutativo
Osservazione.
verde (a)
.
verde (b)
.
azzurro(c).
?-not (verde(c)). [1]
? -not (verde (d)). [2]
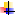 Le mete [1] e [2] riescono perché i fatti
Le mete [1] e [2] riescono perché i fatti
verde(c).
verde (d) .
non sono presenti nel programma
Ma c’è
una differenza concettuale:
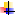 L'oggetto
d non e' presente nel programma, c lo è non è possibile distinguere i due casi
L'oggetto
d non e' presente nel programma, c lo è non è possibile distinguere i due casi
Nota: l'asserzione
"azzurro(c)" non permette di concludere che
c non e' verde, perché non c'e' alcuna informazione sul fatto che"
azzurro" e "verde" sono colori, e che un oggetto ha un unico
colore
Fondamenti concettuali
della negazione per fallimento
Quando una proposizione
A (ad esempio "verde (c) ")
Ø non e presente in un programma
Ø non è derivabile dal programma.
si possono
assumere due posizioni radicalmente diverse:
1) non è noto se A sia vera o falsa
2) A viene ritenuta falsa
Cosa vuol
dire (2): si assume che tutte e sole le
informazioni disponibili siano contenute nel programma.
Ipotesi del mondo
chiuso: regola di inferenza basata su (2)
A non
è dimostrabile
_________________
A è falsa
Ma una
dimostrazione può non terminare! Allora:
Negazione per fallimento finito:
la dimostrazione di A fallisce finitamente
___________________________________
A è falsa
Relazione fra verità e dimostrabilità
in una
teoria assiomatica del primo ordine:
v Se
una proposizione e' vera, è dimostrabile
v Se una proposizione è falsa, vi sono due possibilità:
- la
dimostrazione fallisce in tempo finito
- la dimostrazione non
termina
Negazione Prolog e negazione in logica classica
Logica classica: not(A) e' vero se A e'
falso (non vero)
Prolog: not(G)
e' vera quando G e' falsa, e:
· G e'
completamente istanziata
· la dimostrazione di G fallisce finitamente
Semantica (per grandi
linee)
del
linguaggio delle clausole di Horn
Prolog = linguaggio delle clausole di Horn
+
predicati predefiniti
La Base di un programma P è composta dalle
proposizioni p(A1,…An) (p
predicato) esprimibile a partire da:
- i termini costruiti dai simboli di costante e
funzione di P
- i predicati di P
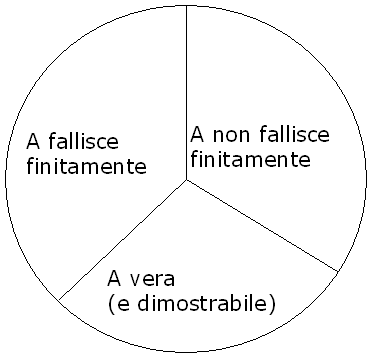
Base del programma
Predicati extra-logici
Predicati Predefiniti per l’Aritmetica
 Il predicato predefinito X is
Expr istanzia la variabile
(libera!) X all’espressione Expr
Il predicato predefinito X is
Expr istanzia la variabile
(libera!) X all’espressione Expr
 Nell’espressione si possono usare le
operazioni aritmetiche e gli operatori di confronto usuali
Nell’espressione si possono usare le
operazioni aritmetiche e gli operatori di confronto usuali
Unificazione
 Il predicato predefinito X = Y ha
successo se X ed Y unificano, ossia se esse sono variabili libere, o se
i termini ai quali sono istanziati unificano. Il
predicato produce effettivamente l’unificazione dei due termini. Ad es., se X/f(K) e Y/f(a), X=Y ha successo producendo l’istanziazione
K/a.
Il predicato predefinito X = Y ha
successo se X ed Y unificano, ossia se esse sono variabili libere, o se
i termini ai quali sono istanziati unificano. Il
predicato produce effettivamente l’unificazione dei due termini. Ad es., se X/f(K) e Y/f(a), X=Y ha successo producendo l’istanziazione
K/a.
 Il predicato X == Y ha successo
se X ed Y sono istanziati a termini identici,
ed effettua solo un controllo (non produce istanziazioni.
Analogamente, X \== Y ha successo se X ed Y non
sono istanziate a termini identici
Il predicato X == Y ha successo
se X ed Y sono istanziati a termini identici,
ed effettua solo un controllo (non produce istanziazioni.
Analogamente, X \== Y ha successo se X ed Y non
sono istanziate a termini identici
Controlli di tipo
 I
predicati predefiniti che controllano il tipo dei termini
sono: integer(X), che ha successo se X è istanziato ad un numero intero, atom(X)
che ha successo se X è istanziato ad una costante non
numerica, constant(X) che ha successo se X è istanziato ad una costante (anche numerica), compound(X) che ha successo se X è istanziato
ad un termine con funtore ed argomenti.
I
predicati predefiniti che controllano il tipo dei termini
sono: integer(X), che ha successo se X è istanziato ad un numero intero, atom(X)
che ha successo se X è istanziato ad una costante non
numerica, constant(X) che ha successo se X è istanziato ad una costante (anche numerica), compound(X) che ha successo se X è istanziato
ad un termine con funtore ed argomenti.
Predicati meta-logici
 Modifiche alla base di dati (assert/retract)
Modifiche alla base di dati (assert/retract)
assert(G) e retract(G) sono predicati metalogici
cioè
predicati del linguaggio che agiscono su proposizioni del linguaggio stesso
§ assert(G)
aggiunge la clausola G al programma
§ retract (G)
rimuove la clausola G dal programma
Conseguenza:
il Modello
del programma cambia in fase di esecuzione
v Cambia
il significato logico del programma
v La
stessa meta, se rieseguita, può dare risultati diversi
In quale caso assert(G)
non influisce sul significato logico del programma? Quando G e' una conseguenza logica! (asserzione di lemmi)
pot(N,0,1):-
!.
pot(N, Exp, P):-Exp1 is Exp-1, pot(N, Exp1 ,P1), P
is N*P1.
?-pot(5, 4, X), assert(pot(5,
4, X)).
Predicati meta-logici
 Ispezione dello stato delle variabili
Ispezione dello stato delle variabili
o var(Term) ha successo se Term è una variabile non istanziata.
Viceversa per nonvar(Term).
 Questi predicati predefiniti consentono di
ispezionare parte dello stato del programma in
esecuzione.
Questi predicati predefiniti consentono di
ispezionare parte dello stato del programma in
esecuzione.
 ?- var(X),
X = a. ha successo, perché
quando viene chiamato var, X non è istanziata.
?- var(X),
X = a. ha successo, perché
quando viene chiamato var, X non è istanziata.
 ?- X = a, var(X. fallisce, perché quando viene chiamato var, X è istanziata.
?- X = a, var(X. fallisce, perché quando viene chiamato var, X è istanziata.
 Quindi, la “,” che sta
in linea di principio per un AND logico, in presenza di predicati extra-logici
può (come in questo caso) non essere più commutativa.
Quindi, la “,” che sta
in linea di principio per un AND logico, in presenza di predicati extra-logici
può (come in questo caso) non essere più commutativa.
 Chiamata di un goal: call(G) invoca il goal G. E’ un predicato meta-logico
perché il suo argomento non è un termine, ossia non è un oggetto del dominio
del programma/teoria logica, ma è un goal, ossia un teorema da dimostrare, che
è un oggetto esterno al programma/teoria logica. Ossia,
il programma invoca dal suo interno il proprio motore inferenziale
su un proprio teorema da dimostrare. Il programma prende così il ruolo
dell’utente di se stesso.
Chiamata di un goal: call(G) invoca il goal G. E’ un predicato meta-logico
perché il suo argomento non è un termine, ossia non è un oggetto del dominio
del programma/teoria logica, ma è un goal, ossia un teorema da dimostrare, che
è un oggetto esterno al programma/teoria logica. Ossia,
il programma invoca dal suo interno il proprio motore inferenziale
su un proprio teorema da dimostrare. Il programma prende così il ruolo
dell’utente di se stesso.
Predicati meta-logici
 Ispezione/costruzione di termini e goal: il
predicato predefinito univ permette di
comporre, scomporre e ispezionare termini e goal, e ha la notazione infissa
“=..”.
Ispezione/costruzione di termini e goal: il
predicato predefinito univ permette di
comporre, scomporre e ispezionare termini e goal, e ha la notazione infissa
“=..”.
 Uso: X =..
[F | L] dove F è un funtore, ed L la lista degli
argomenti. F deve essere istanziato, tutti gli
altri elementi non necessariamente.
Uso: X =..
[F | L] dove F è un funtore, ed L la lista degli
argomenti. F deve essere istanziato, tutti gli
altri elementi non necessariamente.
o
X =.. [p, a, b] o equivalentemente
X =.. [p, [a, b]] supponendo che X sia istanziata, ha
successo se X/p(a,b) oppure se X/p(V,K), producendo V/a,K/b, oppure se
X/p(V,b), producendo V/a, oppure se X/p(a,W), producendo W/b.
o
X =.. [p, a, b] o equivalentemente
X =.. [p, [a, b]] supponendo che X non sia istanziata,
ha successo producendo X/p(a,b).
o
X =.. [p, V, b] o equivalentemente
X =.. [p, [a, b]] supponendo che X non sia istanziata,
ha successo producendo X/p(V,b).
 L’uso X=..[F|L] ha senso in particolare
quando non si conosce o non si vuole considerare l’arità
(numero di argomenti) di F.
L’uso X=..[F|L] ha senso in particolare
quando non si conosce o non si vuole considerare l’arità
(numero di argomenti) di F.
Predicati meta-logici
 Da univ si ricavano i predicati ausiliari
Da univ si ricavano i predicati ausiliari
o functor(Term,F,Arity) che estrae funtore e arità di un termine con
funtore istanziato:
ad es. functor(X,F,Y) con X/p(V,g(H),n) produce
F/p, Y/3
o arg (N,Term,Arg) che estrae l’ennesimo
argomento di un termine: ad es. arg(2,X,A) con
X/p(V,g(H),n) produce A/g(H)
 univ si
può usare per costruire e chiamare goal, come ad es. con la congiunzione G =..
[q, a, g(W)], call(G).
univ si
può usare per costruire e chiamare goal, come ad es. con la congiunzione G =..
[q, a, g(W)], call(G).
 univ si
può usare per manipolare goal, come ad es. con la congiunzione G1 =.. [q, L],
G2 =.. [p, L], call(G2). dove
è stato costruito un nuovo goal con predicato diverso e stessi argomenti.
univ si
può usare per manipolare goal, come ad es. con la congiunzione G1 =.. [q, L],
G2 =.. [p, L], call(G2). dove
è stato costruito un nuovo goal con predicato diverso e stessi argomenti.
Predicati meta-logici
 Il meta-predicato clause(H,B) permette di ispezionare la base di conoscenza del programma. H deve
essere un termine con funtore istanziato.
Il predicato restituisce tutte le regole del programma la cui conclusione
unifica con H, istanziando B con il corpo della
regola, sotto forma di congiunzione.
Il meta-predicato clause(H,B) permette di ispezionare la base di conoscenza del programma. H deve
essere un termine con funtore istanziato.
Il predicato restituisce tutte le regole del programma la cui conclusione
unifica con H, istanziando B con il corpo della
regola, sotto forma di congiunzione.
 Ad esempio, con le clausole:
Ad esempio, con le clausole:
p(a)
:- q(a).
p(X):- f(X),q(X,b).
p(c).
la query ?-clause(p(Y),B). restituisce :
Y/a, B/q(a) e
Y/X, B/(f(X),q(X,b)) e
Y/c, B/true
Si noti che le congiunzioni sono trattate come le
liste, ossia (A,B,C) è equivalente a: ,(A,(B,C)) dove “,”
è considerato un funtore. Non esiste però la “congiunzione
vuota”.
 I predicati meta-logici fanno
sì che il Prolog possa fungere da meta-linguaggio di
se stesso, e permettono di costruire meta-interpreti,
ossia interpreti Prolog scritti in Prolog.
I predicati meta-logici fanno
sì che il Prolog possa fungere da meta-linguaggio di
se stesso, e permettono di costruire meta-interpreti,
ossia interpreti Prolog scritti in Prolog.
Esempio. Uso della ricorsione per attraversare strutture
dati:
Automa a stati finiti ASF
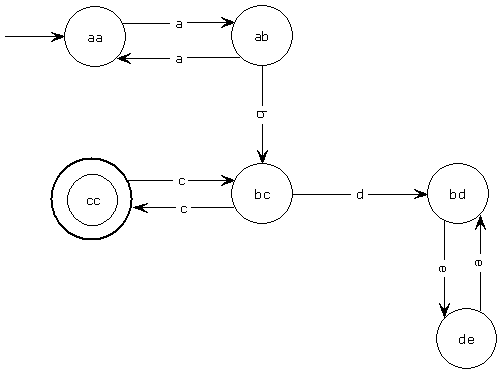
linguaggio
riconosciuto: 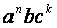 con n e k dispari
con n e k dispari
Rappresentazione "statica"
di un ASF in Prolog
stato_iniziale(aa).
stato_finale(cc)
.
transizione(aa,a,ab).
transizione(ab,a,aa).
transizione(ab,b,bc).
transizione(bc,c,cc).
transizione(cc,c,bc).
Esempio. Simulazione
"dinamica" di un ASF in Prolog
Stringa del linguaggio come lista
es. a³bc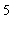 diventa [a,a,a,b,c,c,c,c,c]
diventa [a,a,a,b,c,c,c,c,c]
Il predicato riconosci(+Parola) vale se la parola data e'
accettata dall' automa
 Punto di partenza: stato iniziale
Punto di partenza: stato iniziale
riconosci
(P):- stato_iniziale (S), scandisci (P, S).
 Scansione della parola:
transizioni fino a:
Scansione della parola:
transizioni fino a:
-
termine parola.
- raggiungimento stato
finale
scandisci ( []
,S) :- stato_finale (S), !.
scandisci ([E|L] ,S) :- transizione(S,
E, NS),
scandisci (L,S).
Esempio di uso del backtracking:
elaborazioni su grafi
Colorazione di un
grafo con quattro colori (ad es. rosso, bianco, blu e giallo)
 a ciascun
nodo del grafo e' assegnato un colore
a ciascun
nodo del grafo e' assegnato un colore
 due nodi
adiacenti non hanno mai lo stesso colore
due nodi
adiacenti non hanno mai lo stesso colore
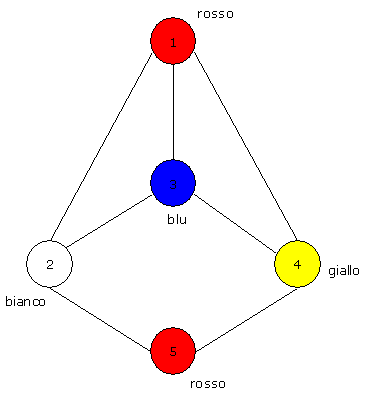
Una strategia
(ingenua) di soiuzione del problema
1. Preso
un nodo non colorato, assegnargli un colore
2. Un
nodo adiacente ha lo stesso colore?
-
se no vai a [6]
3. Tutti
i colori sono stati tentati per il nodo?
- se si
vai a [5]
4. Assegna
al nodo un nuovo colore (non tentato in precedenza) e torna a [2]
5. Esiste
un altro nodo già colorato?
- se si,
vai a [4]
- se no,
vai a [8]
6. Tutti
i nodi sono colorati?
- se no,
vai a [1]
7. Fine
con successo
8. Fine
con fallimento
Soluzione in Prolog
Ø
predicato colora_grafo (+Nadi, ?Col or
azione)
-
Nodi e' la
lista dei nodi det gra_o
-
Colorazione
restituisce le coppie nodo-colore sotto forma di una lista di termini c(N,C) dove N e' istanziato
ad un vertice e C ad un colore
Ø predicato
colora (+Nodi, +Tentativo_Colorazione,
?Colorazione)
e' un
predicato ausiliario, con l'argomento addizionale Tentativo_Colorazione
(inizialmente []) che contiene la colorazione
provvisoria
Ø predicato
colora_nodo(+Nodo, -Colore, +Tentativo_Colorazione)
restituisce un colore Colore
da assegnare al nodo Nodo
Ø predicato
colore_ok (+Nodo, +Colore, + Tentativo_Colorazion vero se
nessun nodo adiacente a Nodo ha colore Colore
Descrizione della
situazione
arco (1
,2) .
arco (1
,3) .
arco (1
,4).
arco
(2,3).
arco
(2,4).
arco
(2,5).
arco
(3,4).
arco
(4,5).
colore
(bianco) .
colore
(rosso) .
colore
(blu) .
colore
(giallo) .
Definizioni
colora_grafo(G, L):-colora(G, [], L).
/* * * * * * * *---- * * *
* * * * *---- * * * * * * * * /
colora([] ,
L, L) :- ! .
colora([N |
R], P, L):- colora_nodo (N,C,P) ,
colora(R, [c(N,C) | P], L).
/* * * * * * * *---- * * *
* * * * *---- * * * * * * * * /
colora_nodo (N,
C, P):- colore (C) ,
colore_ok(N,
C, P).
/* * * * * * * *---- * * *
* * * * *---- * * * * * * * * /
colore_ok(N, C, P):- (arco(N, N1) ; arco(N1 ,N)),
appartiene (c (N1,C), P),
! , fail.
Colore_ok(_ , _ , _).
/* * * * * * * *---- * * *
* * * * *---- * * * * * * * * /
appartiene (E,
[E | X]):- ! .
appartiene (E, [_
| X]):- appartiene(E, X).
Problemi con infinite soluzioni
arco(1 ,2).
arco (2,3).
arco (3,4).
arco (4) 1).
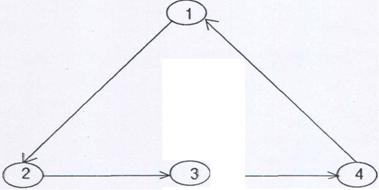
Predicato
cammino
(+Nodo 1, +Nodo2, ?Cammino).
cammino(N1
,N2, [N1 ,N2]):- arco(N1 ,N2).
cammino(N1
,N2, [N1IC]) :-arco(N1 ,N) ,cammino(N,N2,C).
Esistono infiniti
cammini fra due nodi!
Adiacenti:
?- cammino (4, 1, C).
C=[4, 1];
C=[4, 1, 2, 3, 4, 1];
C=[4, 1, 2, 3, 4, 1, 2, 3, 4, 1]
…
Non Adiacenti:
?- cammino(3,1 ,C).
C=[3, 4,
1] ;
C= [3, 4,
1, 2, 3, 4, 1] ;
C=[3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1]
…
Rimedio per evitare le
infinite soluzioni
cammino(N1
,N2, [N1, N2]):- arco(N1 ,N2), ! .
cammino(N1
,N2, [N1 | C):-arco(N1 ,N),
cammino (N,N2,C) , ! .
· il primo ! evita la ricerca di altri cammini se i
nodi sono
adiacenti
?- cammino(4, 1, C).
C=
[4,1];
no
· il secondo ! evita la ricerca di più di un cammino
se i nodi non sono adiacenti
?- cammino(3, 1 ,C).
C=[3,4,1] ;
no
Strutture di selezione
Dati due segmenti [X1,X2] e [Y1,Y2] decidere se hanno intersezione non vuota
X1 |---------------------------| Y1
X2 |---------------------------| Y2
X1
|----------------------------------------------------| Y1
X2|----------------------|
Y2
inters([X1, Y1] ,[X2,Y2]):- X1=<X2, ! , (X2=<Y1 ; Y2=<Y1).
X1 |---------------------------| Y1
X2|--------------------------|Y2
X1|---------------------------------|Y1
X2|-------------------------------------------------------|Y2
inters([X1 ,Y1]
, [X2, Y2]):- X2=<X1, (X1 =<Y2; Y1=<Y2).